CP Algorithms ES

Tabla de contenido

Criba de Eratóstenes

La Criba de Eratóstenes es un algoritmo para encontrar todos los números primos en un segmento $[1;n]$ usando $O(n \log \log n)$ operaciones.

El algoritmo es muy simple: al principio escribimos todos los números entre 2 y $n$. Marcamos todos los múltiplos propios de 2 (ya que 2 es el número primo más pequeño) como compuestos. Un múltiplo propio de un número $x$, es un número mayor que $x$ y divisible por $x$. Luego encontramos el siguiente número que no ha sido marcado como compuesto, en este caso es 3. Lo que significa que 3 es primo, y marcamos todos los múltiplos propios de 3 como compuestos. El siguiente número sin marcar es 5, que es el siguiente número primo, y marcamos todos los múltiplos adecuados. Y continuamos con este procedimiento hasta que procesamos todos los números de la fila.

En la siguiente imagen puede verse una visualización del algoritmo para calcular todos los números primos en el rango $ [1;16]$. Puede verse que, con bastante frecuencia, marcamos los números como compuestos varias veces.

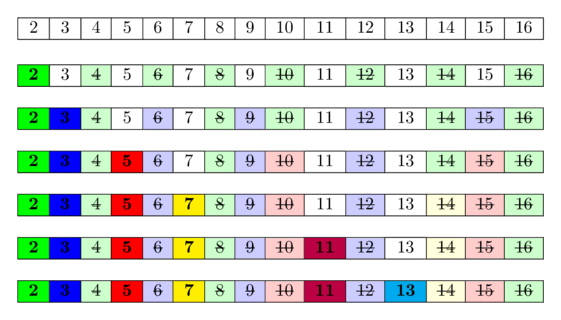
Criba de Eratóstenes

La idea detrás es esta: Un número es primo, si ninguno de los números primos más pequeños lo divide. Dado que iteramos sobre los números primos en orden, ya marcamos todos los números que son divisibles por al menos uno de los números primos como divisibles. Por lo tanto, si llegamos a una celda y no está marcada, entonces no es divisible por ningún número primo más pequeño y, por lo tanto, tiene que ser primo.

Implementación

int n;
vector<char> es_primo(n+1, true);
es_primo[0] = es_primo[1] = false;
for (int i = 2; i <= n; i++) {
    if (es_primo[i] && (long long)i * i <= n) {
        for (int j = i * i; j <= n; j += i)
            es_primo[j] = false;
    }
}

Este código primero marca todos los números excepto el cero y uno como números primos potenciales, luego comienza el proceso de cribado/tamizado de números compuestos. Para esto, itera sobre todos los números desde $2$ a $n$. Si el número actual $i$ es un número primo, marca todos los números que son múltiplos de $i$ como números compuestos, comenzando desde $i^2$. Esto ya es una optimización sobre la forma ingenua de implementarlo, y es válida ya que todos los números más pequeños que son múltiplos de $i$ necesarios también tienen un factor primo que es menor que $i$, por lo que todos ellos ya fueron tamizados antes. Como $i^2$ puede desbordar fácilmente el tipo int, la verificación adicional se realiza usando el tipo long long antes del segundo ciclo anidado.

Usando esta implementación, el algoritmo consume $O(n)$ memoria (obviamente) y realiza $O(n \log \log n)$ (ver la siguiente sección).

Análisis asintótico

Demostremos que este algoritmo toma $O(n \log \log n)$ tiempo. El algoritmo realizará $\frac{n}{p}$ operaciones por cada primo $p \le n$ en el ciclo interno. Por lo tanto, necesitamos evaluar la siguiente expresión:

\[\sum_{\substack{p \le n, \\\ p \text{ primo}}} \frac n p = n \cdot \sum_{\substack{p \le n, \\\ p \text{ primo}}} \frac 1 p.\]

Recordemos dos propiedades conocidas:

Por lo tanto, podemos anotar la suma de la siguiente forma:

\[\sum_{\substack{p \le n, \\\ p \text{ primo}}} \frac 1 p \approx \frac 1 2 + \sum_{k = 2}^{\frac n {\ln n}} \frac 1 {k \ln k}.\]

Aquí extrajimos el primer número primo 2 de la suma, porque $k = 1$ en la aproximación $k \ln k$ es $0$ y causa una división por cero.

Ahora, evaluemos esta suma usando la integral de la misma función sobre $k$ desde $2$ a $\frac n {\ln n} $ (podemos hacer tal aproximación porque, de hecho, la suma está relacionada con la integral como su aproximación utilizando el método del rectángulo):

\[\sum_{k = 2}^{\frac n {\ln n}} \frac 1 {k \ln k} \approx \int_2^{\frac n {\ln n}} \frac 1 {k \ln k} dk.\]

La antiderivada del integrando es $\ln \ln k $. Usando una sustitución y eliminando términos de orden inferior, obtendremos el resultado:

\[\int_2^{\frac n {\ln n}} \frac 1 {k \ln k} dk = \ln \ln \frac n {\ln n} - \ln \ln 2 = \ln(\ln n - \ln \ln n) - \ln \ln 2 \approx \ln \ln n.\]

Ahora, volviendo a la suma original, obtendremos su evaluación aproximada:

\[\sum_{\substack{p \le n, \\\ p\ is\ prime}} \frac n p \approx n \ln \ln n + o(n).\]

Puede encontrarse una prueba más estricta (que da una evaluación más precisa, que es exacta con un multiplicador constante) en el libro de Hardy y Wright “An Introduction to the Theory of Numbers” (p. 349).

Diferentes optimizaciones de la Criba de Eratóstenes

La mayor debilidad del algoritmo es que “camina” a lo largo de la memoria varias veces, solo manipulando elementos individuales. Esto no es muy amigable con el caché. Y debido a eso, la constante que se oculta en $O(n \log \log n) $ es comparativamente grande.

Además, la memoria consumida es un cuello de botella para grandes $n$.

Los métodos que se presentan a continuación nos permiten reducir la cantidad de operaciones realizadas, así como acortar notablemente la memoria consumida.

Tamizado hasta la raíz

Obviamente, para encontrar todos los números primos hasta $n$, bastará con realizar el cribado solo por los números primos, que no superen la raíz de $n$.

int n;
vector<char> es_primo(n+1, true);
es_primo[0] = es_primo[1] = false;
for (int i = 2; i * i <= n; i++) {
    if (es_primo[i]) {
        for (int j = i * i; j <= n; j += i)
            es_primo[j] = false;
    }
}

Dicha optimización no afecta la complejidad (de hecho, al repetir la prueba presentada anteriormente obtendremos la evaluación $n \ln \ln \sqrt n + o(n)$, que es asintóticamente igual según las propiedades de los logaritmos), aunque el número de operaciones se reducirá notablemente.

Tamizado solo por los números impares

Dado que todos los números pares (excepto $2$) son compuestos, podemos dejar de verificar los números pares. En cambio, necesitamos operar solo con números impares.

Primero, nos permitirá tener la mitad de la memoria necesaria. En segundo lugar, reducirá el número de operaciones realizadas por algoritmo aproximadamente a la mitad.

Reducir la memoria consumida

Debemos notar que el algoritmo de Eratóstenes opera con $n$ bits de memoria. Por lo tanto, básicamente podemos reducir la memoria consumida conservando no $n$ bytes, que son las variables de tipo booleano, sino $n$ bits, es decir, $\frac n 8$ bytes de memoria.

Sin embargo, tal enfoque, que se llama compresión a nivel de bits, complicará las operaciones con estos bits. La operación de lectura o escritura en cualquier bit requerirá varias operaciones aritméticas y, en última instancia, ralentizará el algoritmo.

Por lo tanto, este enfoque solo está justificado si $n$ es tan grande que ya no podemos asignar $n$ bytes de memoria. En este caso, intercambiaremos ahorro de memoria ($8$ veces menos) con una ralentización significativa del algoritmo.

Vale la pena mencionar que existen estructuras de datos que realizan automáticamente una compresión a nivel de bits, como vector<bool> y bitset<> en C++.

Criba Segmentada

De la optimización “tamizar hasta la raíz” se deduce que no hay necesidad de mantener todo el conjunto es_primo[1 ... n] en todo momento. Para realizar el tamizado, es suficiente mantener solo los números primos hasta la raíz de $n$, es decir, es_primo[1 ... sqrt (n)], dividir el rango completo en bloques y tamizar cada bloque por separado. Al hacerlo, nunca tenemos que mantener varios bloques en la memoria al mismo tiempo, y la CPU maneja mucho mejor el almacenamiento en caché.

Sea $s$ una constante que determina el tamaño del bloque, entonces tenemos $\lceil {\frac n s} \rceil$ bloques en total, y el bloque $k$ ($k = 0 … \lfloor {\frac n s} \rfloor$) contiene los números en un segmento $[ks; ks + s - 1]$. Podemos trabajar en bloques por turnos, es decir, para cada bloque $k$ revisaremos todos los números primos (desde $1$ a $\sqrt n$) y realizaremos un tamizado usándolos. Vale la pena señalar que tenemos que modificar un poco la estrategia cuando manejamos los primeros números: primero, todos los números primos de $[1;\sqrt n]$ no deberían eliminarse; y segundo, los números $0$ y $1$ deben marcarse como números no primos. Mientras se trabaja en el último bloque, no se debe olvidar que el último número necesario $n$ no es necesario que se encuentre al final del bloque.

Aquí tenemos una implementación que cuenta el número de primos menores o iguales a $n$ usando tamizado de bloques.

int contar_primos(int n) {
    const int S = 10000;

    vector<int> primos;
    int nsqrt = sqrt(n);
    vector<char> es_primo(nsqrt + 1, true);
    for (int i = 2; i <= nsqrt; i++) {
        if (es_primo[i]) {
            primos.push_back(i);
            for (int j = i * i; j <= nsqrt; j += i)
                es_primo[j] = false;
        }
    }

    int resultado = 0;
    vector<char> bloque(S);
    for (int k = 0; k * S <= n; k++) {
        fill(bloque.begin(), bloque.end(), true);
        int start = k * S;
        for (int p : primos) {
            int start_idx = (start + p - 1) / p;
            int j = max(start_idx, p) * p - start;
            for (; j < S; j += p)
                bloque[j] = false;
        }
        if (k == 0)
            bloque[0] = bloque[1] = false;
        for (int i = 0; i < S && start + i <= n; i++) {
            if (bloque[i])
                resultado++;
        }
    }
    return resultado;
}

El tiempo de ejecución del tamizado de bloques es el mismo que el de la criba regular de Eratóstenes (a menos que el tamaño de los bloques sea muy pequeño), pero la memoria necesaria se acortará a $O(\sqrt{n} + S)$ y tenemos mejores resultados de caché. Por otro lado, habrá una división por cada par de un bloque y un número primo de $[1;\sqrt{n}]$, y eso será mucho peor para bloques de menor tamaño. Por lo tanto, es necesario mantener el equilibrio al seleccionar la constante $S$. Logramos los mejores resultados para tamaños de bloque entre $10^4$ y $10^5$.

Encontrar números primos en un rango

A veces necesitamos encontrar todos los números primos en un rango $[L,R]$ de tamaño pequeño (por ejemplo, $R - L + 1 \approx 1e7$), donde $R$ puede ser muy grande (por ejemplo, $1e12$).

Para resolver este problema, podemos utilizar la idea del tamiz segmentado. Pregeneramos todos los números primos hasta $\sqrt R$, y usamos esos primos para marcar todos los números compuestos en el segmento $[L,R]$.

vector<bool> segmentedSieve(long long L, long long R) {
    // generate all primes up to sqrt(R)
    long long lim = sqrt(R);
    vector<bool> mark(lim + 1, false);
    vector<long long> primes;
    for (long long i = 2; i <= lim; ++i) {
        if (!mark[i]) {
            primes.emplace_back(i);
            for (long long j = i * i; j <= lim; j += i)
                mark[j] = true;
        }
    }

    vector<bool> isPrime(R - L + 1, true);
    for (long long i : primes)
        for (long long j = max(i * i, (L + i - 1) / i * i); j <= R; j += i)
            isPrime[j - L] = false;
    if (L == 1)
        isPrime[0] = false;
    return isPrime;
}

La complejidad temporal de este enfoque es $O((R - L + 1) \log \log (R) + \sqrt R \log \log \sqrt R)$.

También es posible que no generemos previamente todos los números primos:

vector<bool> segmentedSieveNoPreGen(long long L, long long R) {
    vector<bool> isPrime(R - L + 1, true);
    long long lim = sqrt(R);
    for (long long i = 2; i <= lim; ++i)
        for (long long j = max(i * i, (L + i - 1) / i * i); j <= R; j += i)
            isPrime[j - L] = false;
    if (L == 1)
        isPrime[0] = false;
    return isPrime;
}

Obviamente, la complejidad es peor, que es $O((R - L + 1) \log (R) + \sqrt R)$. Sin embargo, también funciona muy rápido en la práctica.

Modificación de tiempo lineal

Podemos modificar el algoritmo de tal manera que solo tenga una complejidad de tiempo lineal. Este enfoque se describe en el artículo Criba de Eratóstenes con complejidad de tiempo lineal. Sin embargo, este algoritmo también tiene sus propias debilidades.

Problemas de Práctica

This site is open source. Improve this page.